Dynamical systems describe how things change over time. Imagine a ball rolling down a hill, weather patterns changing day by day, or animals hunting each other—these can all be explained with dynamical systems. They’re like mathematical recipes that tell us how something evolves or behaves as time goes on.
Here’s a breakdown of 9 famous examples from three different categories:
1. Classical Dynamical Systems
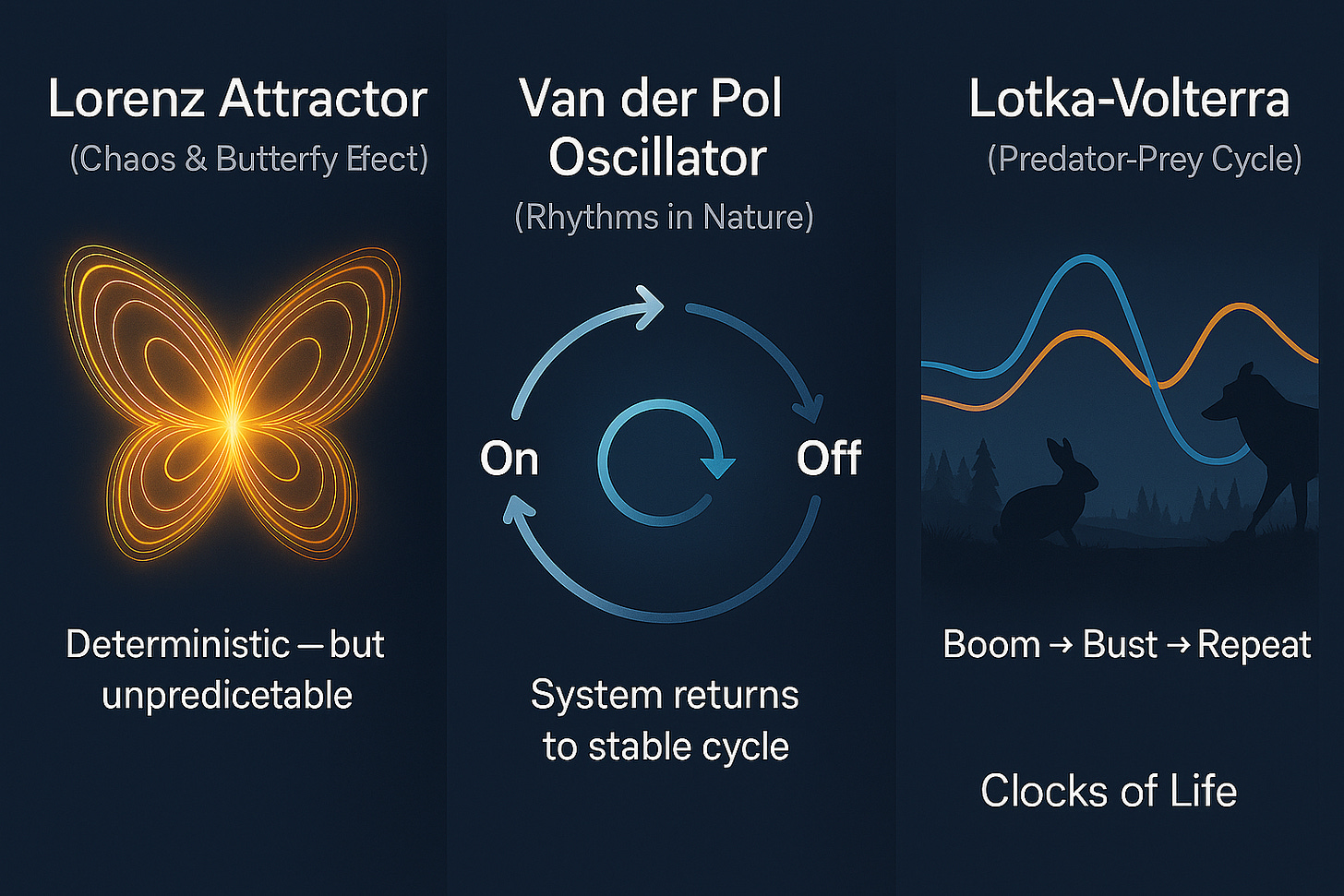
Lorenz Attractor
Imagine a butterfly flapping its wings in Brazil, eventually causing a tornado in Texas. This is an exaggeration, but the Lorenz attractor models how tiny differences in the initial conditions of a system (like weather) can lead to huge differences over time. This idea is popularly known as the “butterfly effect.”
Van der Pol Oscillator
Think about a heartbeat. Normally, it has a steady rhythm, but if it’s disrupted, it tries to return to normal. The Van der Pol oscillator describes systems (like heartbeats or electrical circuits) that naturally find a steady rhythm after disturbances.
Lotka-Volterra (Predator-Prey)
Imagine rabbits (prey) and foxes (predators). When there are lots of rabbits, foxes have plenty to eat, so their numbers increase. But as fox numbers grow, rabbits start to decline because they’re hunted more. Eventually, fewer rabbits mean fewer foxes survive. This creates a constant cycle—rabbits up, foxes up, rabbits down, foxes down, and repeat. Lotka-Volterra equations capture these ups and downs.
Summary:
Lotka-Volterra
Think rabbits and wolves. More rabbits → more wolves → wolves eat rabbits → fewer rabbits → wolves starve → rabbits rebound. This cycle never ends. The Lotka-Volterra model shows how two species interact, creating oscillations that look like waves.
Van der Pol Oscillator
Imagine your heartbeat: it speeds up when you run but always returns to a steady rhythm. That’s what the Van der Pol oscillator models—systems that resist disturbances and restore their rhythm. It applies to heartbeats, neurons, and even circuits.
Lorenz Attractor:
Weather forecasting struggles because of chaos. The Lorenz system shows why: tiny differences in starting conditions—like a butterfly flapping its wings—can lead to completely different outcomes later. This is the “butterfly effect.” It’s deterministic (rules never change) but unpredictable long-term.
2. Biological Dynamical Systems
Phosphorylation Cycles
Think of a protein in your body as a light switch. Adding a phosphate (a tiny chemical tag) turns it “on,” removing it turns it “off.” These switches help your cells respond quickly to signals—like adrenaline causing you to react swiftly when scared.
Toggle Switches
Toggle switches are like a two-way switch in a house: a protein can either be in state A or state B, never in between. It’s either fully on or fully off. This helps cells make clear decisions, like deciding whether a cell should divide or wait.
Oscillators (Biological Clocks)
Your internal body clock is an oscillator—it tells you when to wake up, eat, and sleep, repeating each day. Biological oscillators keep things in sync, just like the rhythmic ticking of a clock.
Summary
Phosphorylation Cycles (Molecular Switches)
Proteins act like light switches in your body. A phosphate tag turns them ON; removing it turns them OFF. These rapid switches control how cells respond to signals—like adrenaline speeding up your heart in danger.
Toggle Switch (Cell Decisions)
Some genes work like rivals. If Gene A is ON, it forces Gene B OFF, and vice versa. This creates bistability—two stable states. It’s how cells make big decisions: become a muscle cell or a neuron, never both.
Biological Oscillators (Clocks of Life)
Your body runs on clocks: heartbeats, circadian rhythms, hormone pulses. These cycles come from feedback loops that switch things on and off in a repeating pattern. Break the rhythm and you feel it—jet lag, fatigue, or worse.
3. Physics Dynamical Systems
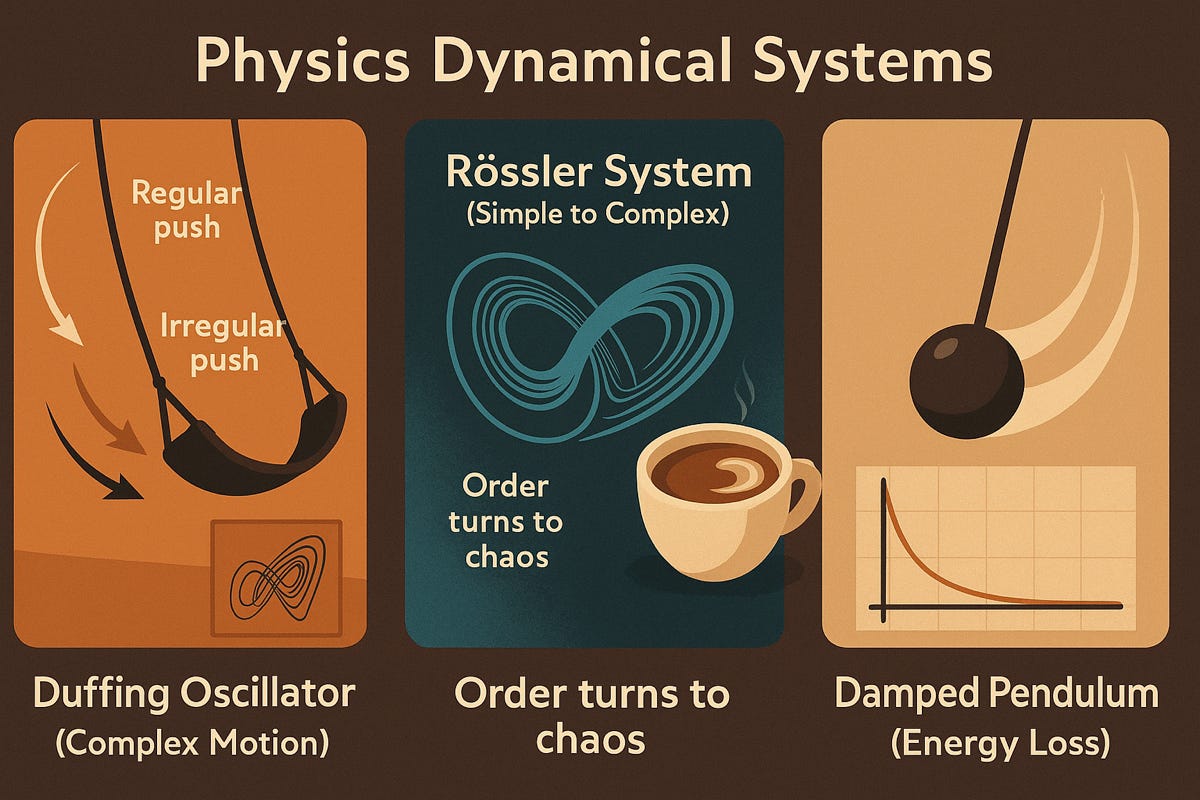
Duffing Oscillator
Imagine pushing someone on a swing, but the swing can behave unpredictably if pushed too hard or at irregular intervals. The Duffing oscillator shows how some systems react in complicated ways when forced beyond their normal limits—sometimes becoming unpredictable or chaotic.
Rössler System
Think of stirring cream into coffee. At first, it’s predictable—cream moves around in a simple swirl. But stir faster and patterns become complex and hard to follow. The Rössler system demonstrates how simple movements can become chaotic and complicated quickly.
Damped Pendulum
Imagine a playground swing that eventually stops because friction slowly takes away its energy. That’s exactly how a damped pendulum works—it gradually loses energy and settles down to rest. This concept is important in understanding how energy dissipates, or “calms down,” over time
Summary
Duffing Oscillator (Complex Motion)
Push a swing gently and it’s predictable. Push harder or irregularly, and things get messy—the swing can move unpredictably. That’s the Duffing oscillator: a system that can flip between stable and chaotic behavior when forced.
Rössler System (Simple to Complex)
Imagine stirring cream into coffee. At first, the swirl is smooth, but speed up and patterns become wild and tangled. The Rössler system shows how simple rules can create complex chaos, similar to turbulence in fluids.
Damped Pendulum (Energy Loss)
Start a pendulum swinging. Each swing gets smaller until it stops—that’s damping, or energy loss. This concept explains friction, how neurons reset after firing, and how proteins relax after working.